十四、时间复杂度

---

 

---

1.定义

算法是解决特定问题求解步骤的描述，在计算中表现为指令的有限序列，并且每条指令表示一个或多个操作

2.特性

1）输入输出

算法具有零个或多个输入，但至少有一个或多个输出

2）有穷性

3）确定性

4）可行性

3.设计要求

1）正确性

2）可读性

3）健壮性

4）时间效率高和存量低

4.算法效率的度量方法

**1）事后统计方法
**

通过设计好的测试程序和数据

利用计算机计时器对不同算法编制的程序的运行时间进行比较，从而确定算法的效率

缺陷：

必须事先编制好测试程序

结果会受到硬件和软件的影响

测试数据设计难

**2）事前分析估算方法
**

在计算机程序编制前，依据统计方法对算法进行估算

一个程序的运行时间，依赖于算法的好坏和问题的输入规模

第一种算法

1. int i = 0, sum = 0, n = 100; //执行1次

2. for(i = 0; i <= n; i++) //执行n+1次

3. {

4. sum = sim + i; //执行n次

5. }

6. printf(“%d”, sum); //执行1次

第二种算法

1. int sum = 0, n = 100; //执行1次

2. sum = (1 + n) * n / 2; //执行1次

3. printf(“%d”, sum); //执行1次

第一种算法执行了1+n+1+n+1=2n+3次，第二种算法执行了3次

再有

1. int i, j , x = 0, sum = 0, n = 100; //执行1次

2. for(i = 1; i <= n; i ++)

3. {

4. for(j = 1; j <= n; j++)

5. {

6. x++; //执行n*n次

7. sum = sum + x;

8. }

9. }

10. printf(“%d”, sum); //执行1次

忽略首尾执行的次数，如果n=100，则循环需要执行100^2^
次，所以此算法的运行时间随着n的增大将远远超过前两种算法

因此，测试运行时间最有效的方法就是计算对运行时间有消耗的基本操作次数

设操作数量为f（n），则有

1）f（n） = n

2）f（n） = 1

3）f（n） = n^2
^

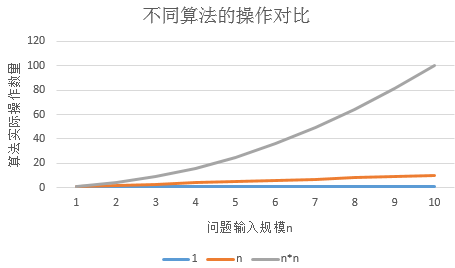
由图中可知，输入规模n越大，算法的效率差异越大

5.函数的渐近增长

1.有算法A执行2n+3次操作，算法B执行3n+1次操作，问哪个算法更快一点？

可得表格为：

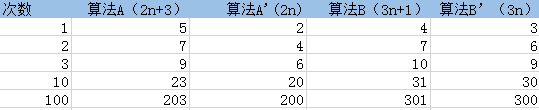
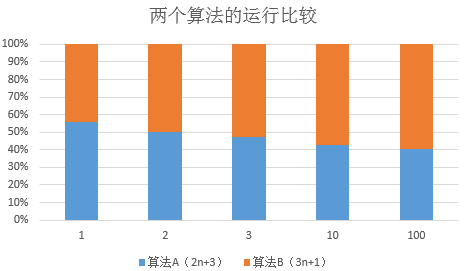
由图可知：

当问题规模n<2时，算法A的效率比算法B低

当n=2时，效率一样

当n>2时，算法A的效率比算法B的效率高

但从总体上看，算法A的效率更优于算法B

由此我们可以得出两个结论：

**1）算法B的渐近增长快于算法A
**

函数的渐近增长：给定两个函数f（n）和g（n），如果存在一个整数N，使得对于所有n>N，

f（n）总是比g（n）大，那么， 我们说f（n）的增长渐近快于g（n）

2）随着n增大，后面的+1+3影响并不大，所以我们可以把后面的常数忽略掉

2.有算法C为2n^2^，算法D为3n+1，算法E为2n^2^+3n+1

得出表格为

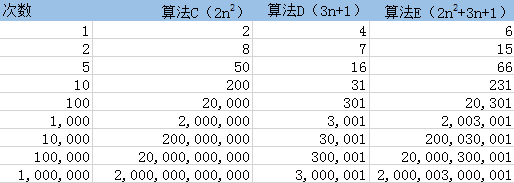
我们发现，

随着n的增大，算法D已经无法跟算法C相比较

且算法D趋于接近算法E

由此得出结论

判断一个算法的效率时，函数中的常数和其他次要项常常可以忽略，而更应该关注主项（最高阶项）的阶数

**某个算法，随着n的增大，它会越来越优于另一算法，或者越来越差与另一算法
**

6.算法时间复杂度

有T（n）=O（f（n））

O（）用来表示时间复杂度，称为大O记法

一般随着n增大，T（n）增长最慢的就是最优算法

之前三个求和算法的时间复杂度分别为O（n）、O（1）、O（n^2^）

1.如何推导大O阶？

1）用常数1取代运行时间中所有加法常数

**2）在修改后的运行次数函数中，只保留最高阶项
**

**3）如果最高阶存在且不是1，则去除与这个项相乘的常数
**

2.常数阶

1. int sun = 0， n = 100; //执行1次

2. sum = (1 + n) * n / 2; //执行第1次

3. sum = (1 + n) * n / 2; //执行第2次

4. sum = (1 + n) * n / 2; //执行第3次

5. sum = (1 + n) * n / 2; //执行第4次

6. sum = (1 + n) * n / 2; //执行第5次

7. sum = (1 + n) * n / 2; //执行第6次

8. sum = (1 + n) * n / 2; //执行第7次

9. sum = (1 + n) * n / 2; //执行第8次

10. sum = (1 + n) * n / 2; //执行第9次

11. sum = (1 + n) * n / 2; //执行第10次

12. printf(“%d”, sum); //执行1次

这段程序一共执行了12次，但时间复杂度为O（1）

3.线性阶

1. int i;

2. for(i = 0; i < n; i++)

3. {

4. //时间复杂度为O（1）的程序

5. }

这段程序的时间复杂度为O（n）

4.对数阶

1. int count = 1;

2. while(count < n)

3. {

4. count = count * 2;

5. //O（1）程序

6. }

每次count乘以2。就更靠近n一点。即有x个2相乘后大于n，就退出循环。由2^x^ =
n可得到x = log2n

所以这个循环的时间复杂度为O（logn）

5.平方阶

1. n++; //执行1次

2. function(n); //执行n次

3. int i, j;

4. for(i = 0; i < n; i++) //执行n*n次

5. {

6. function(i);

7. }

8. for(i = 0; i < n; i++)

9. {

10. for(j = i; j < n; j++) //执行n(n + 1)/2次

11. {

12. //时间复杂度为O（1）的程序

13. }

14. }

最终f（n）=1+n+n^2^+n（n+1）/2 = 3/2n^2^ + 3/2n +
1，时间复杂度为O（n^2^）

7.常见的时间复杂度

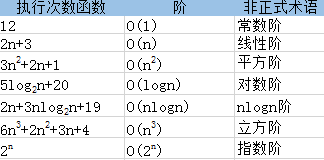
常用的时间复杂度所耗费的时间从小到大一次是：

**O(1)<O(logn)<O(n)<O(nlogn)<O(n^2^)<O(n^3^)<O(2^n^)<O(n!)<O(n^n^)
**

其中O(n^3^)、O(2^n^)、O(n!)、O(n^n^)这一类操作数过大，是不符合实际算法需求的，所以不讨论它们