十、递归

---

 

---

1.定义

一个函数自己直接或间接调用自己

函数之间的相互调用

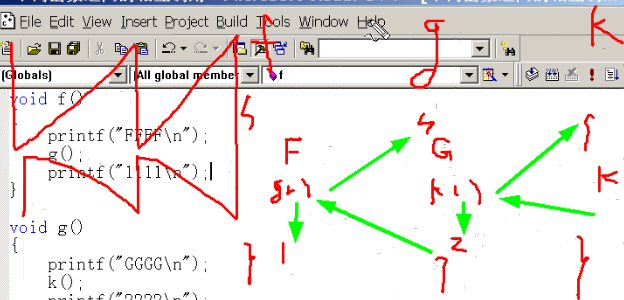
自我调用

1. void f(int n)

2. {

3. if (n == 1)

4. {

5. printf(“哈哈n”);

6. }

7. else

8. f(n - 1);

9. }

2.递归满足的三个条件

1）递归必须得有一个明确的中止条件

2）该函数所处理的数据规模必须在递减

1. void f(int n)

2. {

3. if (n > 7)

4. {

5. printf(“哈哈n”);

6. }

7. else

8. f(n + 1);

9. }

3）这个转化必须是可解的

3.循环和递归

递归：

易于理解，

速度慢

存储空间大

循环：

不易理解

速度快

存储空间小

4.算法示例

1）阶乘

for循环的写法

1. for (i = 1; i <= val; i++)

2. {

3. mult *= i;

4. }

递归的写法

1. long factorial(long n)

2. {

3. if (n == 1)

4. return 1;

5. else

6. return factorial(n - 1) * n;

7. }

当n=3时，f（2）* 3 = f(1) * 2 * 3 = 1 * 2 * 3 = 6

2）1到100的累加

1. int factorial(int n)

2. {

3. if (n == 1)

4. return 1;

5. else

6. return factorial(n - 1) + n;

7. }

3）汉诺塔

 

1. void hanoi(int n, char A, char B, char C)

2. {

3. if (1 == n)

4. {

5. //执行最后把1号盘子移动到最顶端的操作

6. printf(“将编号为%d的盘子直接从%c柱子移动到%c柱子n”, n, A, C);

7. }

8. else

9. {

10. hanoi(n - 1, A, C, B);

11. printf(“将编号为%d的盘子直接从%c柱子移动到%c柱子n”, n, A, C);

12. hanoi(n - 1, B, A, C);

13. }

14. }

或者是

1. void hanoi(int n, char A, char B, char C)

2. {

3. if (n >= 1)

4. {

5. hanoi(n - 1, A, C, B);

6. printf(“将编号为%d的盘子直接从%c柱子移动到%c柱子n”, n, A, C);

7. hanoi(n - 1, B, A, C);

8. }

9. }

其执行顺序图是这样的

类似于树的前序遍历

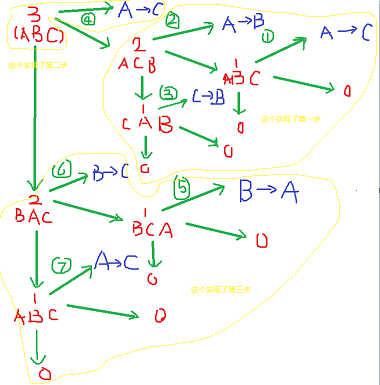
4）间接调用

5.递归的应用

树和森林就是以递归的方式来定义的

树和图的很多算法都是以递归来实现的

很多数学公式就是以递归的方式定义的

1)非波拉契序列：

如果兔子出生两个月后有繁殖能力，一对兔子每个月能生出一对兔子来，假设兔子不死，一年后可以繁殖多少对？

---

经过月数 1 2 3 4 5 6 7 8 9 10 11 12

---

兔子对数 1 1 2 3 5 8 13 21 34 55 89 144

---

可以从这个序列得出，从第三项开始，它等于它前两项之和，因此可得到如下函数：

用常规迭代实现此题的算法为：

1. int main（）

2. {

3. int i;

4. int a[40];

5. a[0] = 0;

6. a[1] = 1;

7. printf(“%d”, a[0]);

8. printf(“%d”, a[1]);

9. for(i = 2; i < 40; i++)

10. {

11. a[i] = a[i - 1] + a[i - 2];

12. printf(“%d”, a[i]);

13. }

14. return 0;

15. }

用递归实现：

1. int Fbi(int i)

2. {

3. if(i < 2)

4. return i = 0? 1 ： 2;

5. return Fbi(i - 1) + Fbi(i - 2);

6. }

2）后缀（逆波兰）表示法

传统的四则运算表达式是这样子的：9+（3-1）*3+10/2，这个称为中缀表示法

将它转换成不需要括号的后缀表示法为：9 3 1 - 3 * + 10 2 / +

那么如何将中缀表达式转化为后缀表达式呢？

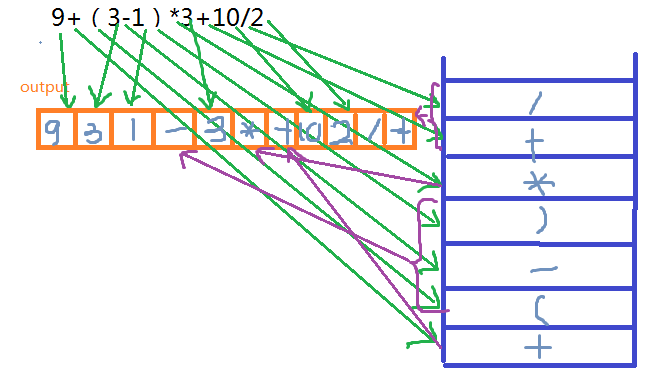
①遇到数字输出，遇到符号压栈，首先输出的是931，压栈+（-）

②当碰到右括号时讲右括号内符号依次出栈，此时输出931-，栈中剩下+

③压栈，输出3，这时遇到+，号的优先级大于+，所以全部出栈，得到931-3*+

④压栈+，输出10，压栈/，输出2，表达式遍历结束，全部出栈，得到最终的后缀表达式

后缀表达式有了，那么如何让机器去阅读并计算表达式呢？

①压栈931，遇到-，则将3和1出栈，1作为减数，3作为被减数，得到2，压栈

②压栈3，遇到，23得6，压栈，又遇到+，6+9得15压栈

③压栈10，2，遇到/，10/2得5压栈

④遇到+，出栈15,5,15+5得20，输出最终结果

这里我们发现，转化时，栈是用来进出符号，计算时，栈是用来进出数字